
Solutions of linear operator equations, in: T. Recurrence, which has solution \(b(n) = B_m + C\). > solve_undetermined_coeffs ( Eq ( a * c * x + a + b, x ),, x ) \) Is more efficient and compact than the Gauss-Jordan method. Then solutions are found using back-substitution. Which results, after elimination, in an upper-triangular matrix. The algorithm used here is fraction-free Gaussian elimination, Note: a localĬopy of the matrix is made by this routine so the matrix that is Unknowns then use solve(Neqs, *Msymbols) instead. If you prefer to enter \(N\) equations and \(M\) Input to this function is a \(N\times M + 1\) matrix, which means it has In that case, all symbols can be assigned arbitrary values. This may cause a situation in which an empty dictionary is returned. In theĬase of underdetermined systems, all arbitrary parameters are skipped. This procedure will return None or a dictionary with solutions. The possible number of solutions is zero, one, or infinite. Solve system of \(N\) linear equations with \(M\) variables, which meansīoth under- and overdetermined systems are supported. solve_linear_system ( system, * symbols, ** flags ) ¶ (A solution for y is obtained because it is the first variableįrom the canonically sorted list of symbols that had a linear > solve_linear ( x + y + z, exclude = ) (y, -x - z) The second element is the solution, not the denominator). Never be a symbol unless a solution for that symbol was found (in which case When the numerator was not linear in any symbol of interest n will (n, d) where n and d are the numerator and denominator of f Solution will correspond strictly to a unique solution. Simplification is done to f other than a mul=True expansion, so the (symbol, solution) where symbol appears linearly in the numerator ofį, is in symbols (if given), and is not in exclude (if given). If the first element of the tuple is not zero, then theįunction is guaranteed to be dependent on a symbol in symbols. (0, 0) meaning that there is no solution to the equation amongst the (0, 1) meaning that f is independent of the symbols in symbols Return a tuple derived from f = lhs - rhs that is one of solve_linear ( lhs, rhs = 0, symbols =, exclude = ) ¶ The output varies according to the input and can be seen by example:įor solving recurrence relationships dsolveįor solving differential equations.
Systems containing relational expressions Systems of linear and polynomial equations Return explicit solutions (if possible) when quintic expressions Return explicit solutions when quartic expressions are encountered. When False, quartics and quintics are disabled, too. Return explicit solutions when cubic expressions are encountered. Guaranteed to find the largest number of zeros possible). Solution with many zeros (instead of using the very slow method When using particular=True, use a fast heuristic to find a System with as many zeros as possible this is very expensive. Instructs solve to try to find a particular solution to a linear Needed if the pattern is inside of some invertible function Other functions that contain that pattern this is only manual=True (default is False)ĭo not use the polys/matrix method to solve a system ofĮquations, solve them one at a time as you might “manually.” implicit=True (default is False)Īllows solve to return a solution for a pattern in terms of

If theįlag is False then nothing will be done to the Floats. Rationals but the answer will be recast as Floats. If rational=None, Floats will be recast as System containing Floats may fail to solve because of issues Recast Floats as Rational if this option is not used, the Make positive all symbols without assumptions regarding sign. General simplify function on the solutions and theĮxpression obtained when they are substituted into theįunction which should be zero. Returning them and (if check is not False) use the Simplify all but polynomials of order 3 or greater before Show a warning if checksol() could not conclude. minimal=True (default is False)Ī very fast, minimal testing. numerical=True (default)ĭo a fast numerical check if f has only one symbol. Useful if you want to include solutions that make anyĭenominator zero. If False, do not do any testing of solutions.
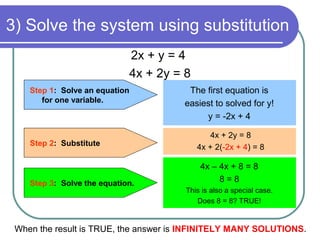
#Substitution system of equations solver free
If expressions are given, the free symbols in them willīe extracted automatically. exclude= (default)ĭo not try to solve for any of the free symbols in exclude

Return list of symbols and set of tuple(s) of solution(s).

Return list (perhaps empty) of solution mappings.


 0 kommentar(er)
0 kommentar(er)
